Write-up

球隊計分

一個蠻簡單的題目，題目有4行輸入、每行有4個數字代表該局得分，1、3行是主隊得分，2、4行是客隊得分，求上下半場的總分跟誰獲勝(Win、Lose、Tie)。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
#include <iostream>
#include <bits/stdc++.h>

int main() {
    int x[4], y[4], w1 = 0, w2 = 0, sum[2] = {0};

    // 上半場
    scanf("%d %d %d %d", &x[0], &x[1], &x[2], &x[3]);
    scanf("%d %d %d %d", &y[0], &y[1], &y[2], &y[3]);

    sum[0] = x[0] + x[1] + x[2] + x[3];
    sum[1] = y[0] + y[1] + y[2] + y[3];
    if (sum[0] > sum[1]) w1 = 1;
    if (sum[0] == sum[1]) w1 = -1;
    printf("%d:%d\n", sum[0], sum[1]);

    // 下半場
    scanf("%d %d %d %d", &x[0], &x[1], &x[2], &x[3]);
    scanf("%d %d %d %d", &y[0], &y[1], &y[2], &y[3]);

    sum[0] = x[0] + x[1] + x[2] + x[3];
    sum[1] = y[0] + y[1] + y[2] + y[3];
    if (sum[0] > sum[1]) w2 = 1;
    if (sum[0] == sum[1]) w2 = -1;
    printf("%d:%d\n", sum[0], sum[1]);

    // 狀態
    if (w1 == 1 && w2 == 1)
        printf("Win");
    else if (w2 == 0 && w2 == 0)
        printf("Lose");
    else
        printf("Tie");

    return 0;
}

路徑和

點我閱讀題目

給出一個N*M的帶權重方陣，要把走過的路的權重都加起來，但是有些限制

只能從權重最小的格子開始
如果有周遭有多個格子可以走，只能走權重最小的
不可以走走過的格子

假設有個4*6的方陣: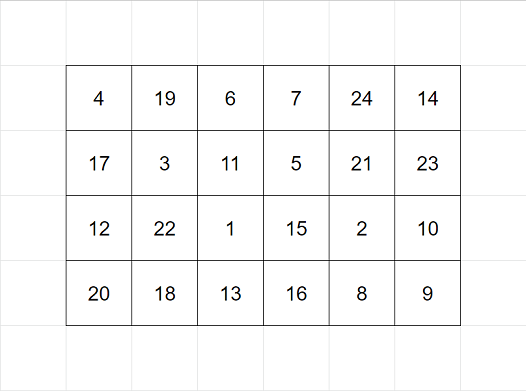 那他的走法會長這樣: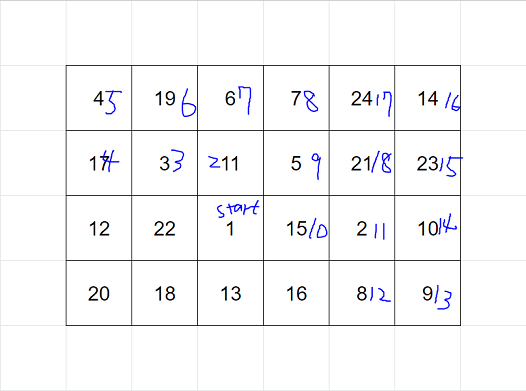

策略先檢查先上下左右的格子可不可以走、有沒有超界，再來看哪個格子最小就往哪裡走!

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
#include <iostream>
#include <bits/stdc++.h>
#define INF 100001

int main() {
    int R, C;
    scanf("%d %d", &R, &C);
    int weight[R][C], visit[R][C]; // 權重 跟 有沒有走訪過(走過會設定成非0)
    int min_pos[2], min; // min_pos = [R, C]

    min = INF; // (題目給的範圍)+1, 這樣就一定可以找到最小值
    for (int i = 0; i < R; i++) {
        for (int j = 0; j < C; j++){
            int w;
            scanf("%d", &w);
            if (w < min) { // 記錄權重最小的格子 出發要用到
                min = w;
                min_pos[0] = i;
                min_pos[1] = j;
            }
            weight[i][j] = w;
            visit[i][j] = 0;

        }
    }

    printf("%d %d\n", min_pos[0], min_pos[1]);
    int flag = 1, ans = 0, pre_r, pre_c, r, c;
    r = min_pos[0];
    c = min_pos[1];
    while (flag) {
        ans += weight[r][c];
        visit[r][c] = 1;
        pre_r = r;
        pre_c = c;
        // printf("R: %d, C: %d, min:%d\n", r, c, min);
        min = INF;
        flag = 0;
        if (pre_r > 0)
            if (visit[pre_r - 1][pre_c] == 0 && weight[pre_r - 1][pre_c] < min) {
                flag = 1;
                min = weight[pre_r - 1][pre_c];
                r = pre_r - 1;
                c = pre_c;
            }

        if (pre_c > 0)
            if (visit[pre_r][pre_c - 1] == 0 && weight[pre_r][pre_c - 1] < min) {
                flag = 1;
                min = weight[pre_r][pre_c - 1];
                r = pre_r;
                c = pre_c - 1;
            }

        if (pre_r < R - 1)
            if(visit[pre_r + 1][pre_c] == 0 && weight[pre_r + 1][pre_c] < min) {
                flag = 1;
                min = weight[pre_r + 1][pre_c];
                r = pre_r + 1;
                c = pre_c;
            }

        if (pre_c < C - 1)
            if (visit[pre_r][pre_c + 1] == 0 && weight[pre_r][pre_c + 1] < min) {
                flag = 1;
                min = weight[pre_r][pre_c - 1];
                r = pre_r;
                c = pre_c + 1;
            }

    }

    printf("%d", ans);
    return 0;
}

我自己覺得這個寫的不是很好，但是也想不到更好的辦法 (つд⊂)

卡通組合

點我閱讀題目

有M個卡通人物，N個卡通團隊 M是一個整數，代表會有幾個字母用來表示人物，len('ABCD....') = M

集合由一字串表示字串中字母可以重複也可以顛倒，ACCDDBBB = {A, C, D, B} 求沒有交集，但是聯集數量為M的集合各數

策略把字串讀進來之後就把它拆成字元丟進Python的set()裡面再用set運算 ~~蝦?你說為什麼用Python? 我就懶癌末期~~

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
M = int(input())
N = int(input())


def break_into_char(string):
    ret = set()
    for a in string:
        ret.add(a)
    
    return ret

sets = []
for i in range(N):
    get_ = input()
    sets.append(break_into_char(get_))

ans = 0
for i in range(N - 1):
    for j in range(i + 1, N):
        if sets[i] & sets[j] == set():
            if len(sets[i] | sets[j]) == M:
                ans += 1

print(ans)

完美彩帶

點我閱讀題目

感謝朋友提供一個很好的解法(Sliding window)!學到新做法了!!

長度為N，顏色數量為M

策略使用一個Dequeue，從front取值、從end新增，列隊內只會一次出現M個顏色，這時只要比對列隊內相異顏色數量是不是等於M就好，是的話這段就是完美彩帶!!

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
#include <iostream>
#include <bits/stdc++.h>

std::map<int, int> occur;
std::deque<int> cols;

int main() {
    int M, N, in, count = 0, ans = 0;

    std::scanf("%d %d", &M, &N);


    for (int i = 0; i < M; i++) {
        std::scanf("%d", &in);
        cols.push_back(in);
        occur[in]++;                    // 顏色出現次數
        if(occur[in] == 1) count++;     // 列隊內顏色總數++
    }

    if (count == M) ans++;              // 如果列隊內相異顏色數量=M 則發現一條完美彩帶

    for (int i = M; i < N; i++) {
        occur[cols[0]]--;               // 取列隊頭，將列隊頭出現次數 - 1
        if (!occur[cols[0]]) count--;   // 如果列隊頭的出現次數=0，代表列隊內顏色總數少1
        cols.pop_front();               // 列隊頭彈出列隊

        std::scanf("%d", &in);          // 讀下個顏色
        cols.push_back(in);             // 下個顏色進列隊
        occur[in]++;                    // 該顏色出現次數+1
        if (occur[in] == 1) count++;    // 列隊內總色數++
        if (count == M) ans++;          // 如果列隊內相異顏色數量=M 則發現一條完美彩帶
    }

    printf("%d", ans);
    return 0;
}

這個解法想像起來還蠻好玩的，就是一個滑動的比對塊w

Write-up:: 201906 APCS 解題過程

APCS 初挑戰心得 (･ω´･ )

Write-up

球隊計分

路徑和

卡通組合

完美彩帶